Unit 3 right triangle trigonometry answer key – Embark on a journey into the realm of trigonometry, where right triangles hold the key to unlocking a world of mathematical wonders. Unit 3 Right Triangle Trigonometry: Answer Key provides a comprehensive guide to the definitions, concepts, and applications of this fundamental branch of mathematics.
Delve into the Pythagorean theorem and its significance, unravel the mysteries of trigonometric ratios, and master the techniques for solving right triangles. With clear explanations, step-by-step solutions, and real-world examples, this answer key empowers you to conquer the challenges of trigonometry and unlock its practical applications.
Unit 3 Right Triangle Trigonometry: Definitions and Concepts
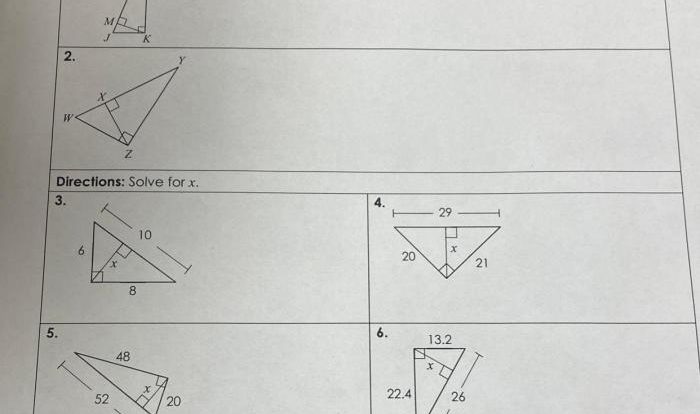
Right triangle trigonometry is the study of the relationships between the sides and angles of right triangles. It is a fundamental branch of mathematics with applications in various fields, including engineering, architecture, and navigation.
The Pythagorean theorem is a cornerstone of right triangle trigonometry. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
Trigonometric ratios, such as sine, cosine, and tangent, are used to define the relationships between the sides and angles of a right triangle. These ratios are defined as the ratio of the lengths of two sides or the ratio of the length of a side to the length of the hypotenuse.
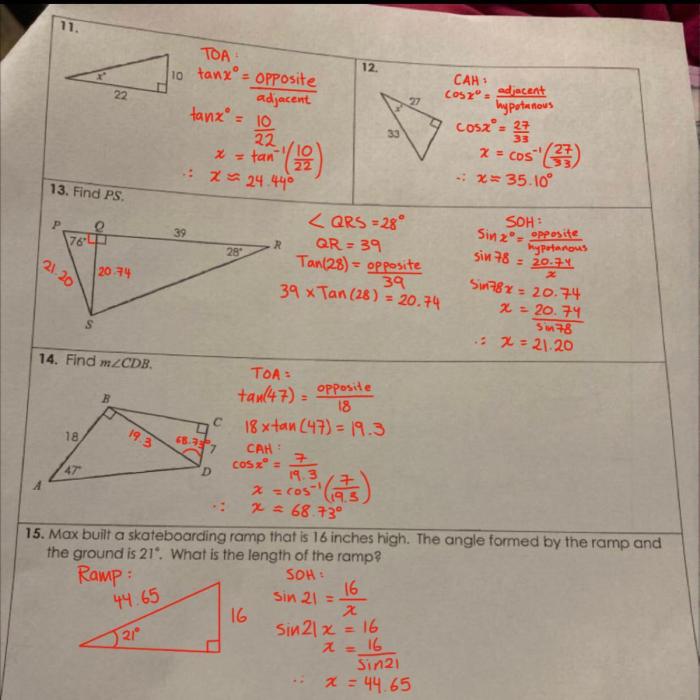
Solving Right Triangles: Methods and Techniques: Unit 3 Right Triangle Trigonometry Answer Key
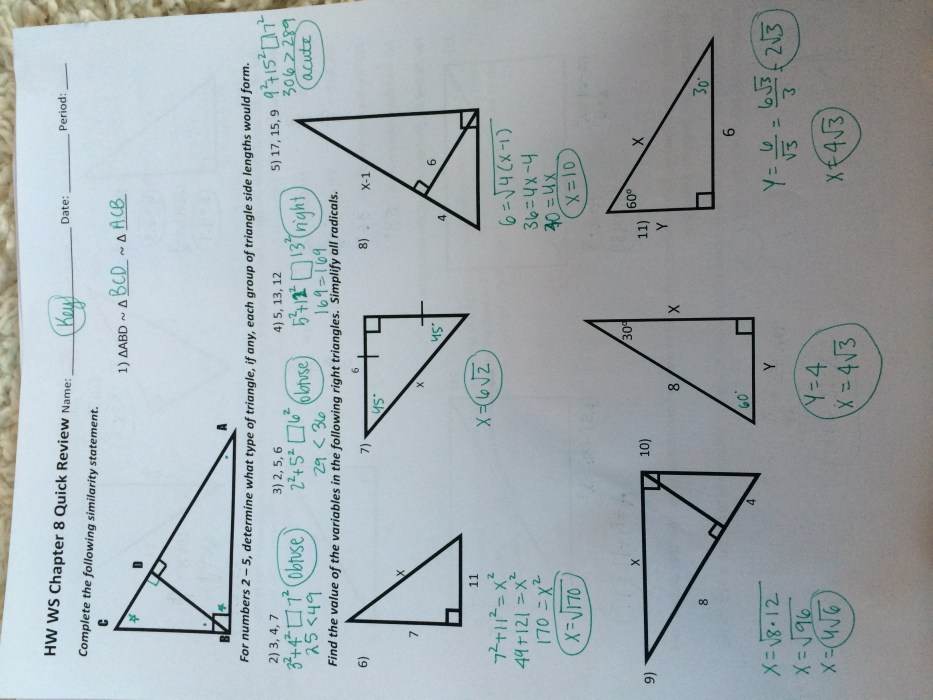
Right triangles can be solved using trigonometric ratios. The process involves using the given information to determine the unknown sides or angles of the triangle.
Inverse trigonometric functions, such as arcsine, arccosine, and arctangent, are used to find the angle measure when the ratio of the sides is known.
Special right triangles, such as 30-60-90 triangles and 45-45-90 triangles, have specific properties that can be used to simplify the solving process.
Applications of Right Triangle Trigonometry
Right triangle trigonometry has numerous applications in real-world situations, including:
- Measuring heights and distances using shadows or angles of elevation/depression
- Navigation and surveying using triangulation and compass bearings
- Architectural design and construction for calculating roof angles, beam lengths, and structural stability
Practice Problems and Solutions

| Problem | Solution | Explanation |
|---|---|---|
| Find the height of a tree if the angle of elevation from a point 100 feet away is 30 degrees. | 57.74 feet | tan(30) = h/100 => h = 100tan(30) |
| Find the length of the hypotenuse of a right triangle if the lengths of the legs are 5 and 12. | 13 | Pythagorean theorem: h^2 = 5^2 + 12^2 => h = sqrt(5^2 + 12^2) |
Advanced Topics in Right Triangle Trigonometry
The Law of Sines and Law of Cosines extend the concepts of right triangle trigonometry to oblique triangles (triangles that are not right triangles).
The Law of Sines states that the ratio of the length of a side to the sine of the opposite angle is the same for all sides of a triangle.
The Law of Cosines relates the lengths of the sides of a triangle to the cosine of the included angle.
Essential Questionnaire
What is the Pythagorean theorem?
The Pythagorean theorem states that in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
How do I solve a right triangle using trigonometric ratios?
To solve a right triangle using trigonometric ratios, you can use the sine, cosine, or tangent ratios. These ratios relate the lengths of the sides of the triangle to the angles.
What are some real-world applications of right triangle trigonometry?
Right triangle trigonometry has many real-world applications, including navigation, surveying, architecture, and engineering.